Light
Light refers to a specific wavelength range within the electromagnetic spectrum. The short-wave end of visible light has a wavelength of about 360-400nm, and the long-wave end is about 760-830nm. Generally, the range is taken as 380-780nm.
Different wavelengths of light can evoke different colour sensations. Isaac Newton used a prism to spatially separate light of different wavelengths. Different positions in a rainbow correspond to different wavelengths, and their “colours” also differ.
Most light we encounter in daily life is complex light, meaning it is not of a single wavelength but is a mixture of multiple wavelengths. Here, an important concept must be mentioned: Metamerism. For the same person, a specific light corresponds to a definite colour, but a specific colour does not correspond to a definite light. Metamerism is the foundation and prerequisite for colour reproduction, which is why it is possible for us to reproduce colours from the natural world on a display, even if the spectra are completely different.
Spectrum
The spectrum is our method for describing the components of complex light.
Light is a form of electromagnetic radiation. We use a radiometric quantity $X$ to measure the amount of radiation. In photometry, radiometric quantities include radiant flux, radiant intensity, irradiance, and radiance, but for now, we can refer to them collectively as radiometric quantity. We want to observe the amount of radiation of different wavelengths within complex light, so we introduce spectral density:
$$X_\lambda = \frac{\mathrm{d}X}{\mathrm{d}\lambda}$$Spectral density can be seen as a function of wavelength. A graph with wavelength on the horizontal axis and spectral density on the vertical axis can vividly represent the spectrum of a light.
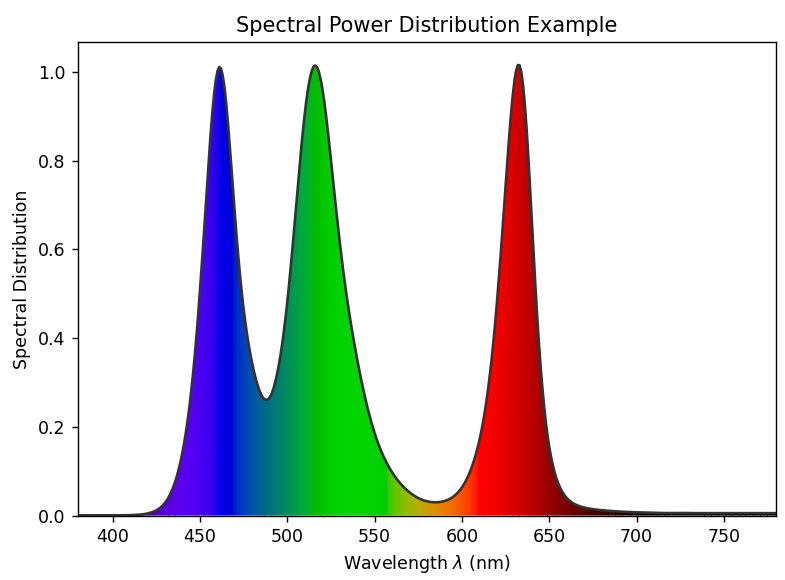
The spectral density distribution is also known as the Spectral Power Distribution (SPD), which, in a narrow sense, refers to the radiant power distribution.
By dividing $X_\lambda$ by $\max{X_\lambda}$, we normalise the SPD so its maximum value is 1. The resulting new function of wavelength is called the relative spectral power distribution.
The Human Eye
Authors Hptim & Jmarchn. - Own work based on: Schematic diagram of the human eye en.svg by Rhcastilhos, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=13572928
The iris automatically adjusts the size of the pupil in the middle according to the intensity of the light. The cornea, lens, aqueous humour, and vitreous humour form the optical structure of the human eye. Cells on the retina perceive light, process and transmit signals, and finally, the nerve impulses are transmitted to the visual cortex via the optic nerve.
As a person ages, the optical density of the lens increases (i.e., its transmittance decreases), especially for shorter wavelengths. This means the lens becomes increasingly “yellow”. Although other parts of the visual system (such as chromatic adaptation) prevent the person from perceiving this change, it can exacerbate metamerism between individuals.
The retina not only converts light signals into nerve impulses but also performs initial processing. Therefore, the retina can be considered an “intelligent image sensor” with on-chip computation. The retina is composed, from inside to out, of receptor cells, bipolar cells, and ganglion cells. The axons of the ganglion cells form the optic nerve, which passes through the blind spot and continues through the retina to transmit signals. This means the retina is actually a “front-illuminated” sensor. The receptor cells related to vision are the cones and rods. Some receptor cells are not related to vision but can still perceive light and participate in other human physiological activities, such as the ipRGCs which are related to circadian rhythms.
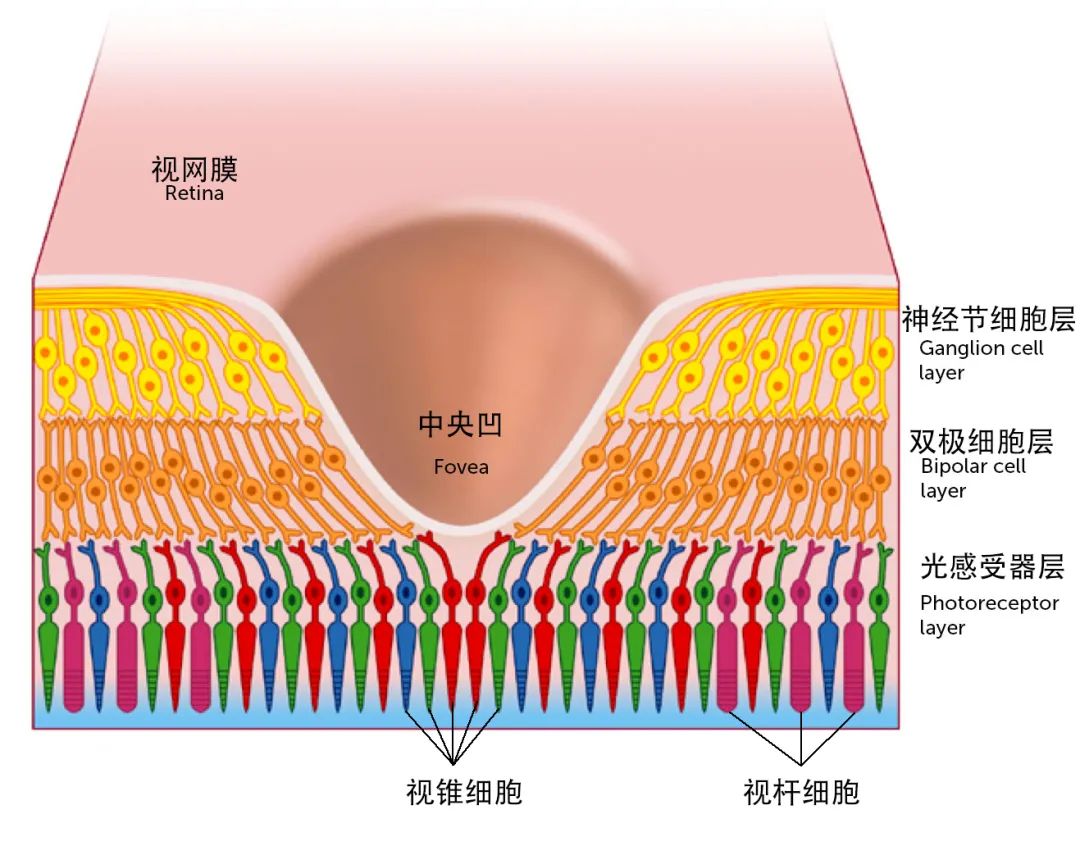
Note that in the diagram, light enters the eyeball from bottom to top. After passing through layers of cells, photopigments at the ends of the receptor cells undergo a light-triggered bioelectrical reaction, converting the light into bioelectrical signals. These signals are then transmitted back to the horizontal, bipolar, and amacrine cell layers. This is a network structure, divided into inner and outer layers, where information is transmitted and processed, before being passed to the ganglion cells, whose axons transmit it to the brain.
Spectral Response of the Human Eye
The pupil and photoreceptor cells of the human eye can automatically adjust and adapt according to the brightness of the ambient light. Based on the working state of the photoreceptor cells, vision can be divided into photopic vision, where cones work alone; scotopic vision, where rods work alone; and mesopic vision, where they work together. The transition from a dark to a bright environment, i.e., from scotopic to photopic vision, is very quick, taking about a minute. However, the transition from photopic to scotopic vision takes about thirty minutes.
For definitions of photopic, scotopic, and mesopic vision, see: A. Stockman and L. T. Sharpe, ‘Spectral Sensitivity’, in The Senses: A Comprehensive Reference, Elsevier, 2008, pp. 87–100. doi: 10.1016/B978-012370880-9.00300-5.
For a photodiode, its responsivity can be defined as the output divided by the input radiant energy. By inputting light of different wavelengths and measuring the output, we can obtain the sensor’s spectral responsivity. For the human eye, this means that light of the same radiant quantity but different wavelengths will have different perceived brightness. However, the output of the human eye cannot be measured directly, so experiments must be designed to relatively measure the perceived brightness of different wavelengths.
The “experiments” mentioned here are one of the most important methods in colour science. Because colour is a human sensation, we call it a “Psychophysical Quantity”. It is not an absolute, objective physical quantity and is also related to a person’s subjective factors. Experiments to measure psychophysical quantities are called psychophysical experiments. Generally, subjects are asked to complete tasks such as rating or matching. If the experiment is poorly designed, giving the subject tasks that are too abstract or difficult, the results will not be good. Furthermore, for experiments that need to represent the common characteristics of all humanity, factors like region and ethnicity must also be considered.
As mentioned earlier, different wavelengths of light give people different colour sensations. So, this experiment can be understood as how to quantify the brightness of different coloured lights with the same radiant quantity, for example, which is brighter between red light and blue light of the same radiant power. For colours with such large differences, observers find it difficult to give stable conclusions. A step-by-step method can be used: the subject repeatedly matches two lights of close wavelengths, covering the entire visible spectrum. Alternatively, the flicker method can be used: two wavelengths of light are flashed alternately. At a frequency of 30-50Hz, if there is a noticeable difference in perceived brightness, the subject will observe a flickering mixed colour. This can be used to judge whether the perceived brightness of the two wavelengths matches. Both methods can yield more stable results.
Let’s temporarily call “perceived brightness” luminous flux $\Phi_v$, and radiant flux $\Phi_e$. Their ratio is the spectral responsivity of the human eye. If we specify a particular wavelength, then:
$$\Phi_v=K(\lambda)*\Phi_e$$Here, $K(\lambda)$ is the spectral responsivity or Luminous Efficacy. By normalising the responsivity over the entire visible wavelength range so that its maximum value is 1, we get a function of wavelength $V(\lambda)$ called the Luminous Efficiency.
The currently used luminous efficiency function was determined by the CIE in 1924 based on experiments with 251 observers. Its maximum value is at 555nm, meaning the human eye is most sensitive to yellow-green light with a wavelength of 555nm. It is important to note that this $V(\lambda)$ recommended by the CIE is fitted from the experimental data of multiple observers; a person with this exact response may not exist in the world. In 1951, the CIE further determined the luminous efficiency function for scotopic vision, $V’(\lambda)$. In scotopic vision, the maximum luminous efficacy is at 508nm, shifting towards the shorter wavelengths. This means that in scotopic vision, humans are less sensitive to long-wavelength light. Mesopic vision simply uses a linear combination of the photopic and scotopic functions.
Data from http://www.cvrl.org/lumindex.htm
Photometry
“Brightness” is actually an ambiguous term. Most lasers are very bright, but if you use a laser to illuminate a room, it is not as bright as a few-watt LED lamp. To eliminate this ambiguity, more precise physical quantities are needed to define “bright”.
Light is a form of radiation. The radiometric quantities mentioned earlier include radiant energy $Q_e$, radiant flux $\Phi_e$, radiant intensity $I_e$, radiance $L_e$, and irradiance $E_e$. Although their names are similar, they are all different physical quantities. After understanding the relationships between these radiometric quantities, photometric quantities can be easily derived, rather than learning a large number of photometric quantities directly as in many textbooks.
Radiometric quantities are physical quantities related to electromagnetic waves and are independent of the human eye; photometric quantities, however, are related to the human eye and are psychophysical quantities.
Radiant Energy and Radiant Flux
Radiant energy: Unit is the joule. It represents the energy of electromagnetic radiation. Electromagnetic radiation is a stream of particles called photons, and the radiant energy is the sum of the energy carried by these photons. The energy of a single photon can be calculated using Planck’s formula: $E=h\nu$, where $h$ is Planck’s constant and $\nu$ is the photon’s frequency.
Radiant flux: Unit is the watt. It represents the radiant energy per unit time. The radiant flux can be obtained by taking the derivative of radiant energy with respect to time. A more intuitive term is radiant power, but to connect with luminous flux, it is recommended to use radiant flux.
Radiant Intensity
Radiant intensity: Unit is watts per steradian.
Let’s first learn about the concept of a steradian. A steradian, $\Omega$, is a unit of solid angle. 1 $\mathrm{sr}$ is defined as the solid angle subtended by an area of $r^2$ on the surface of a sphere. The surface area of a sphere is $4\pi r^2$, so a full sphere corresponds to $4\pi \mathrm{sr}$.
If a point source emits light uniformly in all directions, its radiant intensity is $I_e=\Phi_e/4\pi$. We often say that lasers are “bright”, which not only refers to their potentially high radiant power (e.g., pulsed lasers) but more to their high radiant intensity. This is because lasers are highly directional with a very small divergence angle, resulting in a high radiant intensity in the direction of propagation.
Radiant Exitance and Irradiance
The unit for these quantities is watts per square metre. They measure the different radiant fluxes on a “surface” and can be divided into incident and exiting.
Incident: The radiant flux arriving at a surface is called irradiance. It is calculated by dividing the incident radiant flux by the area.
Exiting: The radiant flux leaving a surface is called radiant exitance. It is calculated by dividing the radiant flux emitted from the surface by the area.
For example, for a piece of grey paper placed under a light, the irradiance is the radiant flux from the light hitting the paper divided by the paper’s area, while the radiant exitance is the radiant flux reflected by the paper divided by the paper’s area. The direction of the incident or exiting light does not matter here, as long as it is the radiant flux arriving at or leaving the surface.
Radiance
Radiance: Unit is watts per steradian per square metre ($W/(sr \cdot m^2)$).
Understanding radiance can be broken down into several steps:
- A surface light source, as distinct from the point source used for radiant intensity, with an area of $\mathrm{d}A$.
- A direction, forming an angle $\theta$ with the normal of the surface source, and a solid angle in that direction of $\mathrm{d}\Omega$.
- In this direction, the projected area of the surface source is $\mathrm{d}A\cos\theta$.
- The radiant flux within this solid angle is $\Phi_e$.
Photometric Quantities
Since the human eye’s perceived brightness varies with the wavelength of light, radiometric quantities cannot directly reflect perceived brightness. Lights of different wavelengths with the same radiance will have different perceived brightness. By multiplying radiometric quantities by the previously mentioned luminous efficiency function, we can define photometric quantities.
Definition: The luminous flux corresponding to a light with a wavelength of 555nm and a radiant power (radiant flux) of 1/683 watts is 1 lumen. By multiplying the radiometric quantities by the luminous efficiency function and the constant 683 lm/W, we obtain the photometric quantities.
- Radiant energy / Radiant flux -> Luminous energy / Luminous flux, with units of lumen-seconds and lumens.
- Radiant intensity -> Luminous intensity, with units of lumens per steradian, defined as a new unit: the Candela (cd), which is one of the base units in the International System of Units.
- Irradiance -> Illuminance, with units of lumens per square metre, defined as the lux (lx).
- Radiant exitance -> Luminous exitance, with units of lumens per square metre.
- Radiance -> Luminance, with units of lumens per steradian per square metre, or candelas per square metre, defined as the nit (nt).
Note that almost every photometric quantity has a new unit defined for it, which can make learning and memorisation difficult. I personally recommend using Candela and Lux in photometry and avoiding Nit.


