光
电磁波中一定波长范围的称为光。可见光的短波端波长约360-400nm，长波端约760-830nm，一般取380-780nm。
不同波长的光能够引发不同的颜色感觉，牛顿利用棱镜将不同波长的光在空间上分开，彩虹不同位置对应着不同的波长，“颜色”也各不相同。
平时能接触到的光，绝大多数光都是复色光，即并非单一波长，而是由多种波长混合出的光。此处需提及一个重要概念：同色异谱 (Metamerism)。对同一个人来说，一种光对应一种确定的颜色，但一种颜色却不能对应一种确定的光。同色异谱现象是颜色再现的基础和前提，所以我们有可能在显示器上再现自然界中的颜色，即使光谱完全不同。
光谱
光谱是我们描述复色光的成分的办法。
$$X_\lambda = \frac{\mathrm{d}X}{\mathrm{d}\lambda}$$
光谱密度可看作关于波长的函数，用横坐标为波长，纵坐标为光谱密度的图表，就能够形象的表示一个光的光谱。
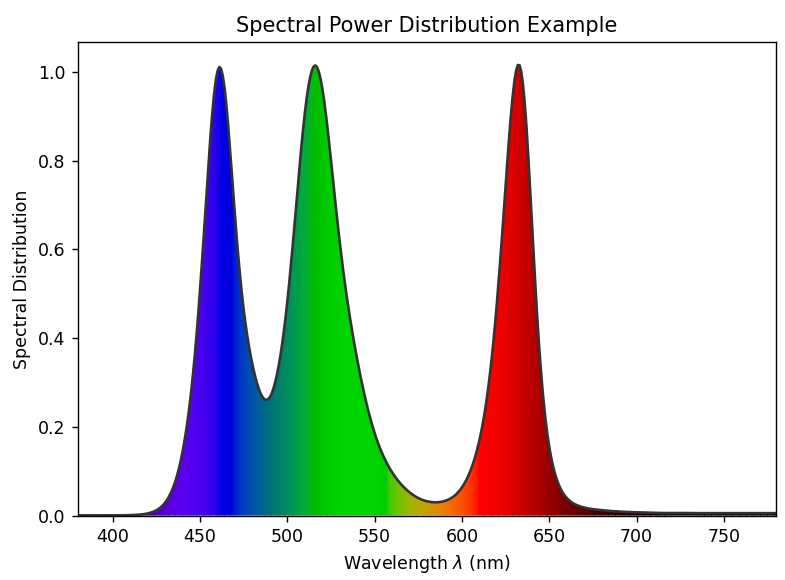
光谱密度分布也可叫做光谱功率分布 (Spectral Power Distribution, SPD)，狭义上是指辐射功率分布。
$X_\lambda$ 除以 $\max{X_\lambda}$，即将SPD归一化，最大值为1，得到的关于波长的新函数称为相对光谱功率分布。
人眼
作者 Hptim & Jmarchn. - 基于如下对象的个人作品： Schematic diagram of the human eye en.svg 由 Rhcastilhos，CC BY-SA 3.0，https://commons.wikimedia.org/w/index.php?curid=13572928
其中，虹膜能够根据光的强弱自动调节中间瞳孔的尺寸，角膜、晶状体、房水、玻璃体组成了人眼的光学结构，视网膜上的细胞能够感知光、处理和传递信号，最后通过视神经将神经冲动传递给视觉中枢。
随着年龄的增大，晶状体的光学密度会增加（即透光率下降），尤其是短波长的部分。即晶状体会变得越来越“黄”，虽然视觉的其他部分（如色适应等）使得人感受不到这样的变化，但会导致人与人之间的同色异谱现象变得严重。
视网膜不仅将光信号转变为神经冲动，还进行了初步的处理，因此视网膜也可以说是有片上运算的“智能图像传感器”。但视网膜由内到外分别是感受器细胞、双极细胞和神经节细胞。神经节细胞的轴突形成视神经，通过盲点再穿过视网膜继续传递，也就是说，视网膜实际上是一种“前照式”传感器。和视觉相关的感受器细胞有视锥细胞 (cones)和视杆细胞 (rods)，有一些感受器细胞与视觉无关，但也能感受光并参与人的其他生理活动，比如和节律有关的ipRGC。
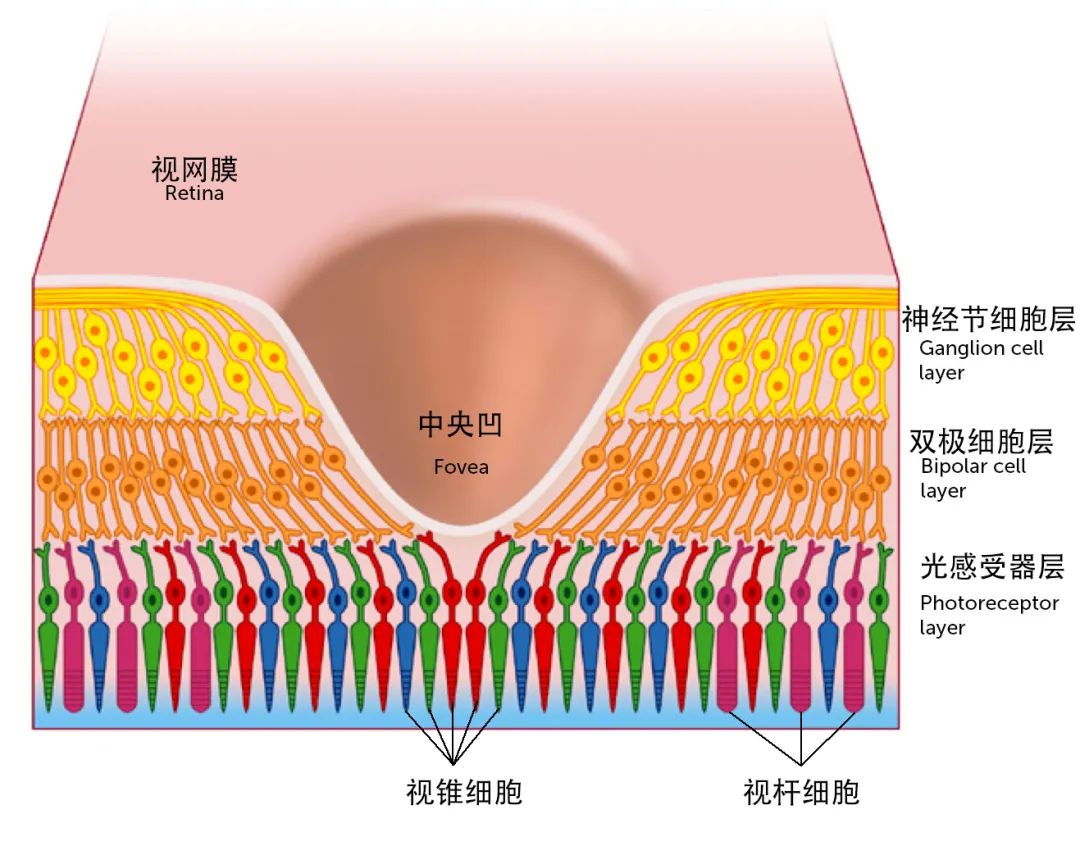
视锥细胞分布在视觉中央很小的区域：黄斑的中央凹。95%以上的视锥细胞集中在这里，视杆细胞又很少分布。除了盲点以外，视杆细胞大量分布在20°视角。正常视觉者的视锥细胞有三种，根据对光的波长的敏感性，分为对长波敏感的L，中波敏感的M和短波敏感的S型，但实际上，由于L和M在基因层面的接近，他们的感光波长峰值比较接近（这可能也是红绿色盲是最常见的色盲的原因）。
关于LMS敏感函数的更多内容，请见http://www.cvrl.org/cones.htm。
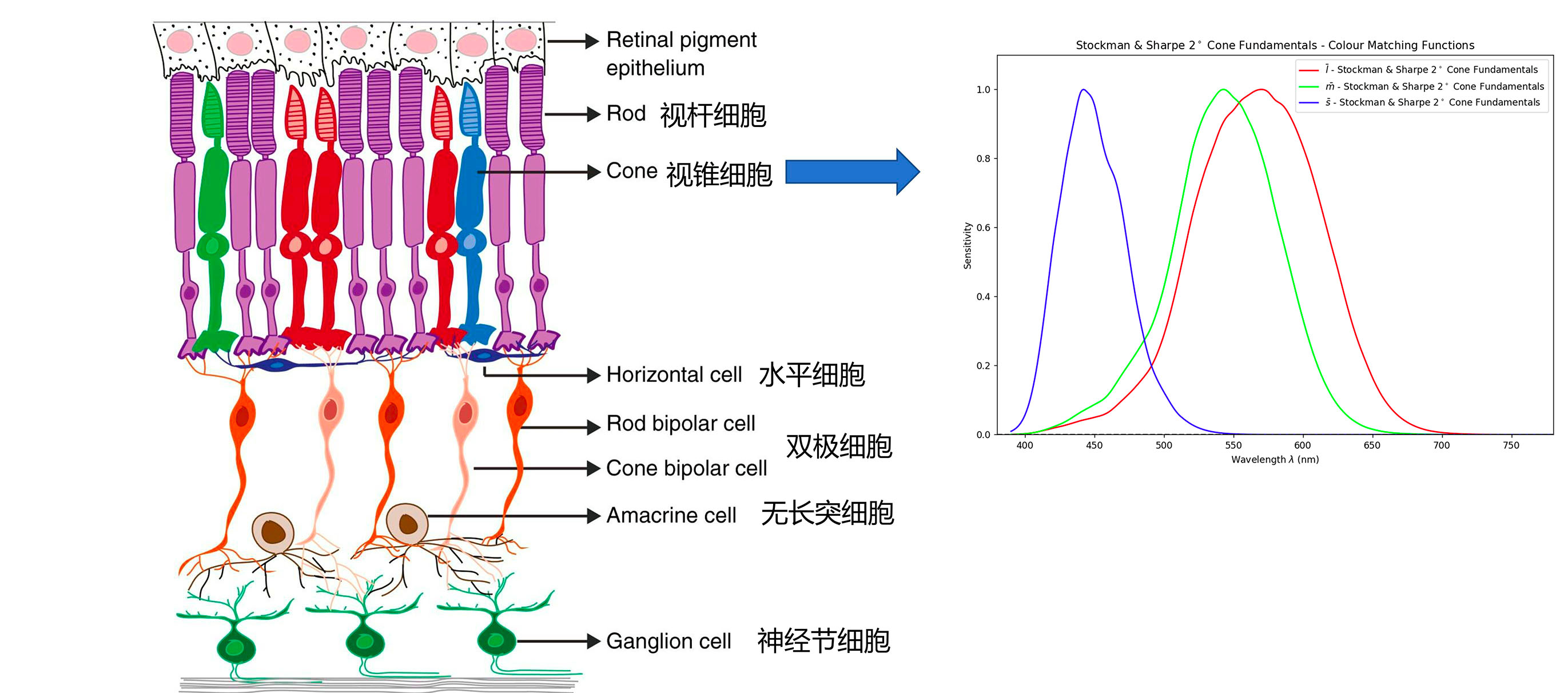
注意图中光是自下而上进入眼球的。光穿过层层细胞后，在感受器细胞的末端上的视色素发生光触发的生物电反应，转化为生物电信号，再反向传递到水平细胞、双极细胞、无足细胞层，这里是网状结构，分内外两层，是信息传递和加工的地方，再传递到神经节细胞，由神经节细胞的轴突传递到大脑。
人眼的光谱响应
根据环境光的亮暗，人眼的瞳孔和感光细胞能够自动调节和适应。其中根据感光细胞的工作状态，可将视觉分为视锥细胞单独工作的明视觉 (Photopic)，视杆细胞单独工作的暗视觉 (Scotopic)和他们混合工作的中间视觉 (Mesopic)。从暗处到明处，由暗视觉转为明视觉的过程很快，大约一分钟就能够完成，但从明视觉转向暗视觉则需要大约三十分钟。
有关明视觉，暗视觉和中间视觉的定义，参见：A. Stockman and L. T. Sharpe, ‘Spectral Sensitivity’, in The Senses: A Comprehensive Reference, Elsevier, 2008, pp. 87–100. doi: 10.1016/B978-012370880-9.00300-5.
对一个光电二极管来说，他的响应度可以定义为输出除以输入的辐射能，使用不同波长的光输入，测量输出值，可以得到传感器的光谱响应度。对人眼来说，就是相同辐射量但不同波长的光，人对其的感知亮度不同。但人眼无法直接测得输出值，因此需要设计实验来相对的衡量不同波长的感知亮度。
此处讲到的“实验”，是色彩科学中几乎最重要的方法，因为色彩是人的感觉，我们将其称为“心理物理量” (Psychophysical Quantity)，他并非一种绝对的客观的物理量，也和人的主观因素有关。测心理物理量的实验称为心理物理实验，一般来说，需要请被试完成一些任务，比如评价，匹配等。如果实验设计的不好，给被试的任务过于抽象或困难，则不能得到很好的结果，另外，一些需要代表全人类共同特点的实验，还需要考虑地区、人种的影响。
之前提到，不同波长的光会给人不同的颜色感觉，所以这个实验可以理解成如何量化相同辐射量的不同颜色光的亮度，比如相同辐射功率的红光和蓝光哪个更亮。对于这样差异大的颜色，观察者实际上很难给出稳定的结论。可以采用分步法：让被试不断匹配两个接近波长的光，分布的匹配整个可见光范围，闪烁法：让两种波长的光交替闪烁，频率为30-50Hz时，如果两种光有较明显的感知亮度差异，被试者会观察到一个亮度闪烁的混合颜色，据此判断两种波长的光的感知亮度是否匹配。这两种方法都能获得更稳定的结果。
我们把“感知亮度”暂时称作光通量 $\Phi_v$，辐射通量为 $\Phi_e$，他们的比值即为人的光谱响应度，如果具体到某一波长，则：
$$\Phi_v=K(\lambda)*\Phi_e$$其中，$K(\lambda)$为光谱响应度或光谱光视效能 (Luminous Efficacy)，对整个可见光波长范围上的响应度做归一化，使其最大值为1，得到的关于波长的函数$V(\lambda)$称为光谱光视效率 (Luminous Efficiency)。
现在使用的光谱光视效率函数时1924年CIE根据251位观察者的实验确定的，其最大值位于555nm，也就是说人眼对波长为555nm的黄绿光最为敏感。需要注意的是，CIE推荐使用的这个$V(\lambda)$是多位观察者的实验数据拟合而成的，世界上并不一定存在这样的人。CIE在1951年进一步确定了暗视觉下的光视效率函数$V’(\lambda)$，暗视觉下，最大视效能位于508nm，整体向短波方向偏移，即暗视觉下，人对长波长的光不太敏感。中间视觉则直接使用明视觉函数和暗视觉函数的线性组合。
数据来自http://www.cvrl.org/lumindex.htm
光度学
“亮度”其实是一个充满歧义的词汇。大多数激光都很亮，但如果用激光来提供室内的照明，他又不如几瓦的LED灯明亮。为了消除这种歧义，就需要更准确的物理量来定义“亮”。
光是一种辐射，之前提到的辐射量，包括辐射能 $Q_e$，辐射通量 $\Phi_e$，辐射强度 $I_e$，辐射亮度 $L_e$，辐射照度 $E_e$。他们虽然名字接近，但都是不同的物理量。理解这些辐射量之间的关系后，可以方便的派生到光度量，而不是像各大教材一样直接学一大堆光度量。
辐射量是与电磁波相关的物理量，和人眼无关；而光度量和人眼有关，是心理物理量。
辐射能和辐射通量
辐射能：Radiant energy，单位是焦耳。表示电磁辐射的能量，电磁辐射是光子组成的粒子流，光子所携带的能量的总和就是辐射能。一个光子的能量可以用普朗克公式计算：$E=h\nu$，其中$h$是普朗克常数，$\nu$是光子的频率。
辐射通量：Radiant flux，单位是瓦。表示单位时间的辐射能量，辐射能对时间求导即可得到辐射通量。更直观的说法是辐射功率，但为了和光通量联系，建议使用辐通量。
辐射强度
辐射强度：Radiant intensity，单位是瓦每球面度。
我们先来学习一下球面度的概念，球面度 $\Omega$ 是一个立体角单位，1$\mathrm{sr}$定义是球面上面积为$r^2$的区域所对应的立体角。一个球的表面积是$4\pi r^2$，一个球面对应的$4\pi sr$。
如果一个点光源均匀的向四周发光，那么其辐射强度$I_e=\Phi_e/4\pi$。我们常说激光很“亮”，不仅指激光的辐射功率可能很大（比如脉冲激光），更多是指激光的辐射强度大，因为激光的方向性很强，发散角极小，在激光传播方向上的辐射强度很大。
辐射出射度和辐照度
这些量的单位都是瓦每平方米，衡量“表面”上的不同辐射通量，可分为入射，出射。
入射：即到达一个表面上的辐射通量，称为辐射照度 (Irriadiance)，计算方式是到达表面的辐射通量除以面积。
出射：从一个表面离开的辐射通量，称为辐射出射度 (Radiant exitance)，计算方式是从表面发出的辐射通量除以面积。
比如一张灰色的纸，放在灯光下，辐射照度是灯光照射到纸上的辐射通量除以纸的面积，而辐射出射度就是纸反射出的辐射通量除以纸的面积。此处入射或出射的光是什么方向都可以，只要是到达或离开表面的辐射通量。
辐射率（辐射亮度）
辐射亮度或辐射率：Radiance，单位是瓦每球面度每平方米 ($W/(sr*m^2)$)。
理解辐亮度，可分为几个步骤：
- 一个面光源，区别于辐射强度时用到的点光源，面积是$\mathrm{d}A$。
- 一个方向，与面光源的法线夹角为$\theta$，该方向上的一个立体角是$\mathrm{d}\Omega$。
- 这个方向上，面光源的投影面积是$\mathrm{d}A\cos\theta$。
- 这个立体角内的辐射通量是$\Phi_e$。
光度学量
由于人眼对不同波长的光的感知亮度不同，因此辐射度量并不能直接反映人眼的感知亮度。辐亮度相同的不同波长的光会有不同的感知亮度。将辐射量乘上之前提到的光视效率函数，可以定义光度量。
定义：555nm波长，辐射功率（辐射通量）为1/683瓦的光对应的光通量为1流明。把之前的辐射量乘上光视效率函数和常数683 lm/W，就得到了光度量。
- 辐射能/辐射通量 -> 光能量/光通量，单位是流明秒和流明。
- 辐射强度 -> 发光强度，单位是流明每球面度，定义为一个新的单位：坎德拉 (Candela)，是国际单位制中的基本单位之一。
- 辐射照度 -> 光照度，单位是流明每平方米，定义为勒克斯 (Lux)。
- 辐射出射度 -> 光出射度，单位是流明每平方米。
- 辐亮度 -> 亮度，单位是流明每球面度每平方米，或坎德拉每平方米，定义为尼特 (Nit)。
注意到几乎每个光度学量都定义了新的单位，这其实给学习和记忆带来了困难，个人推荐在光度学中使用Candela和Lux，避免使用Nit。
